1行で
遷移を工夫した山登り法によって、強いデッキを高速に編成するアルゴリズムを構築しました。
はじめに
はじめまして。9月の上旬に2週間、データサイエンティストコースのインターンに参加した長沢です。普段はKaggleや競技プログラミングにうつつを抜かしており、企業のインターンに参加したのは今回が初めてです。
この記事では、インターン中に私が取り組んだ内容について書きます。機械学習が流行ってるけど組み合わせ最適化も良いぞということが伝われば良いなと思います。
本記事の概要
デッキの良さを示す指標を作り、制約を整理して問題の定式化を行います。解の発見にMIPソルバが有効か確認をした後、山登り法を使って最適化を行い、現行手法と編成デッキの比較を行います。
取り組んだ課題
逆転オセロニア

逆転オセロニア
「逆転オセロニア(以下オセロニア)」というタイトルはどなたも聞いたことがあるのではないでしょうか。名前の通り、オセロをモチーフとした2人対戦型のゲームですが、オセロニアにはトレーディングカードゲームのような「デッキ」の概念があります。
プレイヤーは所持するキャラクター駒から1枚(リーダー1枚+他15枚)を選び、可能な限り「強い」デッキを作って対戦に挑みます。駒によってはデッキ内の他の駒の属性がスキル発動の条件になったりするため、闇雲に強い駒ばかりを入れるのではなく、駒同士の相性を考慮してデッキを作る必要があります。また、駒ごとにコストが設定されており、デッキ内でのコストの合計値は一定の値以下である必要があります。
オススメ編成
オセロニアには「オススメ編成」という機能があります。これは自動的にデッキを作ってくれる機能で、
- 使用したい駒(0〜15枚)
- デッキ属性(神デッキ、魔デッキ、竜デッキ、混合デッキ、指定なし)
- デッキコスト
を指定すると、残りの駒を上手く決めてくれます。
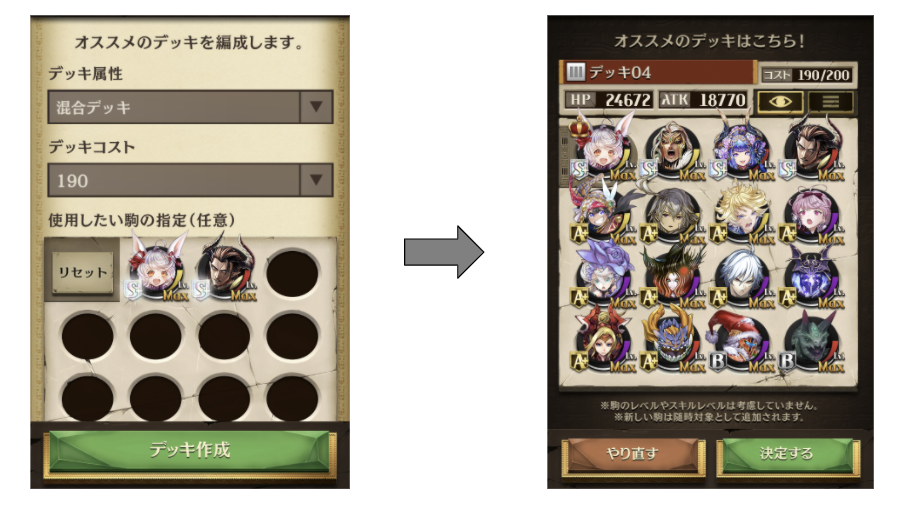
オススメ編成(※現在の環境では異なる可能性があります。)
現行のオススメ編成機能は、貪欲法(良さそうな駒をどんどん選び、条件を満たしたら完成)に近いようなアルゴリズムを使っています。これを改善し、より良いオススメができるか?というのが、私の取り組んだ課題でした。
デッキ評価関数の設計
早速最適化と行きたいところですが、現状は「何が良いデッキなのか?」ということを表す指標がありません。そこで、まずデッキの評価関数を設計します。(実際には最適化と評価関数の設計を交互に進めます。)
最適化の過程で何度も計算することになるため、評価関数は計算コストが低い方が良いです。したがって、重い機械学習モデルなどは使いづらいです。
結論を書くと、「デッキ内の16枚の駒で作れる全てのペアの関係スコアの総和」を目的関数としました。事前準備として、オセロニアに登場する全ての駒から2枚を選ぶ全ての方法について関係スコアを定めます(オセロニアに登場する駒の種類を全4000種とするなら4000×4000の表を作ることになります)。デッキの評価時には、デッキから2枚選ぶ全ての方法(${}_{16}C_2$通り)について表を参照し、全ての関係スコアを足し合わせ、デッキの評価値とします。これを最大化することを、今回の目標にしました。
数式でそれっぽく書くと以下のようになります。$R_{xy}$は駒$x$と駒$y$の関係スコアを表します。
$$ \underset{deck}{\text{maximize}} \sum_{1 \le i \lt j \le 16} R_{deck_i deck_j} $$
「関係スコア」はアソシエーション分析の結果を使って手動で調整しましたが、今考えるとここに機械学習が入る余地はあったかもしれません。
アソシエーション分析の結果を使用することについては、現行の手法を踏襲しています。詳しくは 『逆転オセロニア』におけるAI活用を振り返る - Speaker Deck をご覧ください。
インターンではさらに一方の駒がリーダーかどうかによってスコアの場合分けを行いましたが、今回の記事では省略します。
デッキ編成問題の定式化
制約の整理
ここで、最適化の制約を一旦整理してみます。目的関数も少し書き直します。
目的関数
$$ \text{maximize}\sum_{1 \le i \lt j \le M} R _{ij} y _{ij} $$
$M$は、手持ちの駒の数を表す定数です。$y_{ij}$は、手持ちの駒の中で$i$番目の駒と$j$番目の駒が両方デッキに使われていることを示す01変数です。また、$R_{ij}$を、手持ちの$i$番目の駒と$j$番目の駒の関係スコアと定義し直しています。
ペア制約
(20/10/15追記: Twitterにてご指摘をいただき、式を修正しました。ご指摘、ありがとうございました。)
$$ y_{ij} \le x_i \left( 1 \le i \lt j \le M \right) \\\ y_{ij} \le x_j \left( 1 \le i \lt j \le M \right) $$
$x$ は、手持ちの$i$番目の駒を使うことを表す01変数です。この制約により、$x_i$と$x_j$の少なくとも一方が0なら、$y_{ij}$ は0となります。(逆は成り立ちませんが、$R_{ij}$が非負であれば問題ありません。)
枚数制約
$$ \sum_{i=1}^M x_i = 16 $$
デッキ作成に使う駒は16枚です。
コスト制約
$$ \sum_{i=1}^{M} cost_i x_i \le C $$
$cost_{i}$は、手持ちの$i$番目の駒のコストを表す定数です。$C$は、ユーザの設定したコストの上限を表す定数です。
同一駒制約
$$ \sum_{j \in S_i} x_j \le L_i (1 \le i \le W) $$
オセロニアでは、同一種類の駒(進化前・進化後なども同一とみなされる)は使用枚数に制限があります。この制約はその制限を表しています。$S_{i}$は同一とみなされる駒のグループを表しており、$L_{i}$は使用枚数の上限を表します。$W$はグループの総数です。
デッキ属性制約(神デッキ指定の場合)
$$ \sum_{i \in God} x_i \ge 10 $$
ユーザがデッキ属性を指定した場合、このような制約が追加されます。
おおよそ以上のように定式化されます。(実際にはリーダーについての制約も必要です。)また、こうしたゲームルールの制約に加えて、実用上「最適化に時間をかけ過ぎてはいけない」という制約もあります。
改めてデッキ編成の制約全体を俯瞰すると、この最適化問題は制約と目的関数がすべて一次式で表され、変数は整数の値を取ることがわかります。このような問題は整数計画問題などと呼ばれます。連続変数が混ざる場合を含めて**混合整数計画問題(MIP)**と呼ばれることも多いです。
MIPソルバで解けるか?
一般に、組み合わせ最適化の問題は、最適解を得ることが難しい場合が多いです。(ナップザック問題や最小費用流問題のように、効率的に解けるアルゴリズムが存在する場合もあります。)今回の問題も、最適解を効率的に計算することは難しそうです。残念。
しかし、ここで油断してはいけません。混合整数計画問題を解くための道具として、MIPソルバと呼ばれる種類のソフトウェアが存在します。MIPソルバは、制約と目的関数を与えると、最適解を探してくれるソフトウェアです。内部には組み合わせ最適化のあらゆる叡智が詰まっています。うっかり高速に最適解が求められてしまうかもしれません。
実際に今回の問題で使ってみると、
- ユーザの所持する駒が少ない(3桁程度)場合はすぐに最適解が得られる
- 所持駒が多い(4桁程度)場合は数時間かけてもソルバが止まらない
という結果になりました。人類の叡智といえど流石に最適解は難しかったようです。
山登り法で最適化
ようやく本命です。
前述の通り、組み合わせ最適化の問題は最適解を得ることは難しいです。しかし、最適でなくとも、実用十分な近似解を得るだけなら難易度は大きく下がります。
近似解を得る方法として、焼きなまし法、山登り法、ビームサーチなどのアルゴリズムが挙げられます。今回は、
- 解に順序が無い(ある場合はビームサーチが強い)
- 時間制限が短い(長い場合は焼きなまし法が強い)
- 良い近傍を定義しやすい(良いデッキは少し変えてもやはり良いデッキ)
といった理由により、山登り法を使うことにしました。
山登り法とは
山登り法は、
- まず適当な初期解を用意し、暫定解とする。
- 次の操作を繰り返す。
- 暫定解を少し変えて新しい解を作る。
- 新しい解が暫定解よりも良い解であれば、暫定解を新しい解で更新する。
- 改善できなくなったら(または制限時間に達したら)終了
というアルゴリズムです。今回の問題に適用するなら、
- まず適当にデッキを作り、暫定デッキとする。
- 次の操作を繰り返す。
- 暫定デッキを少し変えて新しいデッキを作る。
- 新しいデッキが暫定デッキよりも良いものであれば、暫定デッキを新しいデッキで更新する。
- 改善できなくなったら(または制限時間に達したら)終了
と言い換えられます。
山登り法でキモとなるのは、
- 暫定解(デッキ)を少し変えて新しい解(デッキ)を作る。
の部分です。「解を少し変える」方法をどう選ぶかによって、山登り法の性能は大きく変わります。
「解を少し変える」方法を考える
シンプルな方法として、暫定デッキから1枚、暫定デッキ外から1枚を選び、交換するという方法が思いつきます。これでもそこそこ良いデッキは作れそうですが、うまくいかない場合もあります。うまくいかない場合について考えます。
最大コスト200で探索を進め、暫定解が「コスト20の駒×4、コスト10の駒×12」となっている場合を考えます。この時、さらに解の改善を繰り返すことでより目的関数の数値が大きい「コスト20の駒×5、コスト10の駒×9、コスト5の駒×2」のデッキに到達することはできるでしょうか。
差分で考えると、コスト10-10-10の3枚をコスト20-5-5の3枚に置き換える必要があることがわかります。ここで1枚を交換する方法の場合を考えると、
- コスト10の駒からコスト20の駒への交換は、最大コストを超過してしまうため起こり得ない
- コスト10の駒からコスト5の駒への交換は、(コスト5の駒はコスト10の駒より弱いため)目的関数の値が改善せず、起こりにくい
となります。シンプルな1枚交換による山登り法では、本来存在するより良い解に到達しにくい場合があることがわかります。
「3枚を置き換える必要があるなら、『暫定デッキと暫定デッキ外から3枚を選んで交換し、目的関数の値が改善したら暫定デッキを更新』としたら良いのでは?」といったことも考えられます。しかし、デッキ内外から3枚ずつ選ぶ組み合わせは、もしユーザの所持駒が1000枚なら${}_{16}C_{3}{} \times {}_{1000}C_{3} ( \gt10^{10})$通り程度あり、探索に時間がかかってしまうため、この方法は使いづらいです。
局所解から抜け出せない問題を解決する方法として「山登り法の代わりに焼きなまし法を使う」という方法もありますが、今回は「解を少し変える」方法を工夫することで解決を試みます。
Variable Depth Search とは
「解を少し変える」方法として、**Variable Depth Search (VDS)**と呼ばれる種類の手法を使います。日本語では可変深度探索と呼ばれるようです。巡回セールスマン問題に対するLin–Kernighan法は、VDSの代表的な例です。
VDSは、ざっくりと言えば**「解が改善しそうかによって深さを制限する深さ優先探索」**となります。とはいえ実際にどのように使えるのか、これでは想像がつかないと思うので、今回のデッキ最適化問題に適用した場合の動作例を説明します。
VDSでは、あらかじめパラメータとして最大探索深さと一時的に緩和する制約条件を決めておきます。今回は最大3枚を変更すれば良さそうと考え、最大探索深さは3、一時的に緩和する制約として最大コストを+10と決めます。
先程と同様に、最大コストを200として、コスト10-10-10の3枚がコスト20-5-5の3枚に入れ替わる例を考えます。現在、合計コストが200、目的関数(スコア)が1500となる暫定解が得られているとします。

合計コスト200、スコア1500
深さ1
まず、1枚交換の場合と同じように、1枚を交換してスコアが改善する場合を探します。この時、もし何も工夫せずとも交換してスコアが改善した場合は、この回の探索を終了して暫定デッキを更新します。
工夫無しにスコアが改善しなかった場合、あらかじめ決めていた緩和した制約を使って、スコアが改善する方法があるか探します。もし改善する方法が見つからなければ山登り法が終了となります。緩和した制約のもとでスコアが改善したなら、一時的に暫定デッキを置き換えて次のステップ(より深く探索)に進みます。
下図は、コスト10の駒ひとつをコスト20の駒で置き換え、スコアが300改善したが合計コストが10超過している状態です。緩和した制約を満たしつつスコアが改善しているので、次のステップに進みます。

合計コスト210、スコア1800
深さ2
一時的にひとつの駒を置き換えた暫定デッキから、さらに駒をひとつ入れ替えて、当初のスコア(1500)と比べスコアが改善するデッキがあるか探します。この時、駒を入れ替えることでスコアが改善し、かつコストが200以下であるデッキが見つかれば、この回の探索を終了して暫定デッキを更新します。
そのようなデッキが見つからなかった場合、緩和した制約のもとでスコアが当初より改善する方法を探します。もし改善する方法が見つからなければ、一時的に交換していた駒を元に戻し、1ステップ戻ります(1枚交換してスコアが改善する他の方法を探します)。
緩和した制約のもとでスコアが当初より改善したなら、さらに暫定デッキを一時的に置き換え、次のステップに進みます。
下図は、コスト10の駒をコスト5の駒で置き換え、スコアが当初より200改善したが合計コストが5超過した状態です。緩和した制約を満たしつつスコアが改善しているので、次のステップに進みます。

合計コスト205、スコア1700
深さ3
一時的にふたつの駒を置き換えた暫定デッキから、さらに駒をひとつ入れ替えて、当初のスコアと比べスコアが改善するデッキがあるか探します。
深さがあらかじめ決めた上限に達しているため、今回は緩和した制約は使わず、元の制約のみを使います。
もしデッキの制約を満たしつつ、スコアが当初より改善する方法が見つかれば、この回の探索を終了して暫定デッキを更新します。見つからなければ、一時的に交換していた駒をひとつ元に戻し、1ステップ戻ります(2枚交換してスコアが改善する他の方法を探します)。
下図は、コスト10の駒をコスト5の駒で置き換え、スコアが当初より100改善した状態です。

合計コスト200、スコア1600
デッキの制約を満たしつつスコアが当初より改善しているので、この回の探索を終了し、暫定解を更新します。

暫定デッキの更新
ここまでで山登り法の「解を少し変える」方法の1ステップとなります。少しと言いつつ長かったですね。
さて、VDSを使ったことで、山登り法の性質はどのように変わったでしょうか。
まず、1枚交換だけを行う方法と比べて、より広く解を探すことができ、局所解に陥りにくくなりました。そして、2枚以上を単に選んで交換する方法と比べて、より効率良く解の改善を行うことができるようになりました。
結果
同条件で、山登り法と現行手法との比較を行います。
比較がしやすくなるよう、2〜3枚を指定して、同じテーマのデッキができるようにします。候補となる駒は、あるランク300のユーザの所持駒(およそ2000種)とします。
代償デッキ
- [美と愛の女神]ヴィーナス
- [トリート解法]メーティス
- [道を切り開く者]ネイト
を指定します。

代償デッキ(背景にかっこいい感じの線を入れようとしたらオセロじゃなくて囲碁になってしまった)
全体として、山登り法の方はバランスの良いデッキとなっているようです。
現行手法で入っている「ジークフリート」「ハーピストエンジェル」「フェリタ&プティ」「ブレスドソーディアン」「オキクルミ」は代償デッキに入りやすい駒ではない (神単の駒が混ざってきている) のに対して、山登り法ではすべての駒が代償デッキとして機能しています。
竜デッキ
- [二重星の竜魔術士]デネヴ
- [地城竜]ランドタイラント
を指定します。

竜デッキ
この条件では、2手法に大きな差はありませんでした。
吸収デッキ
- [断罪の鬼鋸]千代
- [世界を問う者]ルシファー
を指定します。

吸収デッキ(一部画像を加工しています)
現行手法で入っている「リリティエ」「翡翠」「サキュバス」「イヴェット」が吸収デッキに入りやすい駒ではない (魔単の駒が混ざってきている) のに対して、山登り法ではすべての駒が吸収デッキとして機能しています。
また、山登り法ではコスト5の駒が入った上で完成度の高いデッキを編成できています。コスト5の駒を入れられたのはVDSのおかげといえそうです。
探索時間について
山登り法は300msec~500msec程度でデッキを構築することができました。また、今回の実装では探索時に全ての駒を候補として探索しましたが、実際に対戦において有用な駒は限られるため、候補を絞ることでより高速なデッキ構築が可能と考えられます。
まとめ
本記事では、オセロニアのデッキ構築を、組み合わせ最適化の問題と捉えて解く方法を紹介しました。手法として解の改善にVariable Depth Searchを行う山登り法を使用し、結果として400msec程度で良いデッキを構築できることが確認できました。
昨今では多くの問題の解決に機械学習が使われています。しかし、問題の内容によっては、古典的な組み合わせ最適化の手法は依然として強力です。本記事が皆様の抱える問題に対する解決手法選択の一助となれば幸いです。
おまけ
今回使用した
- MIPソルバ
- Variable Depth Search を使った山登り法
は、実はどちらもKaggleのSanta’s Workshop Tour 2019(https://www.kaggle.com/c/santa-workshop-tour-2019 )というコンペティションの解法として登場しました。興味のある方はぜひ調べてみてください。そしてKaggle沼にはまりましょう。
オセロ・Othelloは登録商標です。TM&© Othello,Co. and MegaHouse / © 2016 DeNA Co.,Ltd.








最後まで読んでいただき、ありがとうございます!
この記事をシェアしていただける方はこちらからお願いします。